Эссе Гай ПалмЯ не очень разбираюсь в музыке! Что ж, может я кое-что знаю ... но не так много. Я вообще не играю ни на каких инструментах, и я не математик или ученый звуковых частот. Но ... в то же время, несмотря на отсутствие у меня музыкального образования, семизначная октава "До-Ре-Ми" музыкальных звуков, столь популярная в западной музыке, была так же хорошо вбита в мою голову, как и любой другой человек, живущий в мире, который использует 7-нотную диатоническую / 12-нотную хроматическую музыкальную систему, популярную во многих странах Запада. И ... конечно ... идея октавы - или тонов, входящих и не совпадающих по фазе друг с другом с предсказуемым интервалом частоты -, конечно, неизбежна для любого - даже для тех, кто не знает первую. вещь о музыке.
Так называемая «октава» - интересное явление природы. Идея прогрессии, которая заканчивается на ноте, которая похожа, но все же отличается, напоминает мне о геометрической прогрессии, представленной в другом месте в этом исследовании, где девятиступенчатая последовательность геометрических форм ведет нас от точки к сфере ... где , благодаря нашему признанию бесконечно релятивистской шкалы размеров, мы способны рассматривать сферу как просто еще одну начальную точку бесконечного подъема ... (или спада, если двигаться в обратном направлении). Идея о том, что точка и сфера, по сути, одинаковы, но при этом имеют очевидные различия, в сочетании с идеей музыкальной октавы,
Семь нот шкалы «До-Ре-Ми» действительно прекрасны, но ... как нумеролог, я не мог не задаться вопросом, что бы произошло, если бы кто-то охватил это пространство между концами шкалы восемью нотами вместо Семь; т.е. восемь нот, из которых девятая, по сути, такая же, как первая, но все же отличается в плане ее восхождения по шкале частот? Мне было любопытно. Я должен был сам услышать, насколько разумно или ужасно звучала бы гамма музыкальных нот, если бы они завершились в восемь шагов, с девятой нотой в фазе с первой, вместо семи шагов, с восьмой нотой в фазе. с первым. Можно ли вставить еще одну ноту в существующую октаву? Или вставка всего одной дополнительной ноты настолько испортила бы ритм сакральной геометрии музыки, что превратила бы получившуюся гамму в бесполезный атональный беспорядок из негармоничного шума? Я хотел знать.
В процессе поиска я немного искал девятиступенчатые музыкальные гаммы, но ничего не нашел. Я обнаружил несколько случаев, когда люди играли разные стили музыки в пределах девяти выбранных нот ... но это всегда были только девять нот, выбранных из стандартных двенадцати нот хроматической музыкальной записи, а не девять совершенно уникальных частот, которые охватывают феномен «октаву» по-своему. Я столкнулся с чем-то, называемым «Секретной» шкалой сольфеджио, но это было менее чем удовлетворительное решение. Итак, я продолжил поиск. Я нашел некоторые другие методы настройки, которые включали более семи или двенадцати тонов, но ни один из них не был основан на девяти. По общему признанию, я не стал так усердно искать, и ... после того, как не смог найти ни одной существующей шкалы из девяти нот, которые выглядят как та, которую я создал здесь, Я решил создать эту девятитональную «октаву» самостоятельно. Если я воссоздал то, что уже известно миру музыки, это полное совпадение. Поскольку эта шкала просто логарифмически делит «октаву» на девять, вполне возможно, что такая октава уже существует, а я ее просто не нашел. В любом случае, будь я первым, кто сделал это или просто еще одним в длинной череде любопытных людей, результирующая серия тонов - это то, что это исследование Таро, нумерологии, сознания, космологии и музыки считает совместимым с девятью числами, используемыми для обозначьте теоретическую модель существования, представленную повсюду в этом исследовании. Если эти тона непригодны для создания музыки, ничего страшного. Они все еще могут служить тональными или аудиофоническими представлениями девяти чисел нумерологии.
-----
Тональное сообщениеЯ не историк, особенно музыки. Но, исходя из того, что я узнал до сих пор, похоже, что двенадцатиточная хроматическая система западной музыки представляет собой более или менее фиксированную систему установленных звуковых частот, которые используют многие инструменты для равной настройки. Она называется шкалой равной темперации из-за того, как она распределяет ноты равномерно, логарифмически, в диапазоне октавы. Очевидно, что для вставки хотя бы одной дополнительной ноты в такую фиксированную систему потребуется настройка всех установленных частот, чтобы освободить место для этой одной дополнительной ноты. Для уха, обученного распознавать установленные тональные частоты, выбранные из-за их красоты, неудивительно услышать жалобы на любыеизменение частоты как «неправильное» или «расстроенное». В то же время, однако, есть и другие упомянутые выше методы настройки, которые уже используются ... или не используются, но, по крайней мере, изобретены. Фактически, есть люди, которые думают, что шкала Equal Temperament «расстроена», и предпочитают продвигать альтернативу, которая вносит небольшие корректировки в эти установленные частоты, чтобы добиться более идеально чистого тона для каждой ноты. Итак, идея играть музыку с серией тонов, которые не совсемсоответствовать тем, которые можно найти на средней западной фортепианной клавиатуре, не ново, и, следовательно, не обязательно "неправильный" поступок. Это, безусловно, утешение, потому что в противном случае шкала из девяти тонов считалась бы расстроенной, если бы не гибкость музыки, позволяющая принимать различные виды настройки и разные виды нот. Точно так же именно такая гибкость ума и слуха потребуется от любого, кто читает это эссе или слушает получающиеся тоны девятиступенчатой шкалы. Любой, кто думает, что семь нот системы двенадцати нот западной музыки - это единственное наиболее совершенное и священное произнесение звуков, когда-либо задуманных, и что их не следует никаким образом изменять, вероятно, должен прекратить читать прямо сейчас ... и позволить любопытным продолжать.
Когда я экспериментировал с тонами и пытался «вписать» другой тон в последовательность из семи, я обнаружил некоторые интересные аномалии восприятия звука. Во-первых, поскольку мое ухо, как и многие другие, было настроено на систему из семи и двенадцати нот западной музыки, все мои первоначальные попытки вставить дополнительную ноту провалились просто потому, что этой новой ноте некуда было деваться в моем предубежденном уме. "красивые тона". Все попытки скорректировать существующие ноты, чтобы освободить место, только приводили к тому, что эти некогда красивые ноты звучали ровно и расстроенно. Независимо от того, насколько близко я подошел к настройке этих семи нот, чтобы они по-прежнему звучали достаточно близко, всегда была одна нота, которая звучала как драндулет. Казалось, что охватить «октаву» восемью нотами вместо семи невозможно, без того, чтобы хотя бы одна из этих нот звучала плоско и неуместно. Но что было действительно странно, так это то, как в некоторых случаях я мог заставить серию из восьми нот звучать довольно хорошо в качестве возрастающей шкалы, но ... когда я воспроизводил их в порядке убывания, был тот один драндулет, который не поместиться. И ... если бы я отрегулировал частоты так, чтобы та же самая гамма звучала хорошо в порядке убывания, когда я играл ее в порядке возрастания, та же самая нота, которая предположительно была зафиксирована и, казалось, подходила, теперь звучала бы как драндулет в другом направлении. . Некоторое время я ходил туда-сюда, внося небольшие поправки в существующую семерку, чтобы уместить восьмую ноту. Это никогда не работало. Кто-то может сказать, что это не так Это работает, потому что семь нот, которые я редактировал, являются наиболее совершенным и священным произнесением звуков из когда-либо придуманных, и пытаться «отрегулировать» их - мерзость. Но я столкнулся с другой аномалией восприятия, которая заставила меня усомниться в этой мудрости.
Субъективный характер восприятия интересен, особенно когда речь идет о музыкальных нотах, которые были объявлены красивыми. По мере продолжения экспериментов я обнаружил еще один интересный результат, который заставил меня задуматься о красоте специальных нот. Это эксперимент, который каждый может провести с любым стандартным клавишным инструментом, например, с фортепиано. Попробуйте сыграть мелодию, в которой используются только черные клавиши. Или просто поиграйте с черными клавишами, проигрывая любую случайную последовательность. Поиграйте с этими нотами тридцать секунд, минуту или больше. Тогда ... попробуйте внезапно включить одну из белых клавиш. Просто случайным образом нажмите одну из белых клавиш примерно через тридцать секунд после того, как услышите только черные клавиши. Когда я это сделал, выбранная мною нота звучала ужасно плоско и неуместно ... и все же я включил ноту, которая предположительно была одной из "красивых" ноты священной последовательности идеально красивых нот. Как это возможно, чтобы такая красивая нота могла звучать так плоско и ужасно? Я думаю, что ответ ... контекст ... и то, как установленный контекст может создать предубеждение комфорта, которое не хочет нарушаться. Что удивительно, так это то, как разуму требуется всего несколько секунд, чтобы приспособиться к новому контексту звуков, из-за чего член предыдущего контекста комфорта может затем стать незваным гостем. Точно так же эта идея контекстуального предубеждения должна быть преодолена, чтобы воспринимать любую другую шкалу тонов как их собственный контекст тонов, а не как что-то просто "неправильное" или "расстроенное" по отношению к некоторые другие предубеждения относительно тональных предпочтений. Как это возможно, чтобы такая красивая нота могла звучать так плоско и ужасно? Я думаю, что ответ - это ... контекст ... и то, как установленный контекст может создать предубеждение к комфорту, которое нельзя нарушать. Что удивительно, так это то, как разуму требуется всего несколько секунд, чтобы приспособиться к новому контексту звуков, из-за чего член предыдущего контекста комфорта может затем стать незваным гостем. Точно так же идея контекстного предубеждения должна быть преодолена, чтобы воспринимать любую другую шкалу тонов как их собственный контекст тонов, а не как что-то просто «неправильное» или «расстроенное» по отношению к некоторые другие предубеждения относительно тональных предпочтений. Как это возможно, чтобы такая красивая нота могла звучать так плоско и ужасно? Я думаю, что ответ ... контекст ... и то, как установленный контекст может создать предубеждение комфорта, которое не хочет нарушаться. Что удивительно, так это то, как разуму требуется всего несколько секунд, чтобы приспособиться к новому контексту звуков, из-за чего член предыдущего контекста комфорта может затем стать незваным гостем. Точно так же идея контекстного предубеждения должна быть преодолена, чтобы воспринимать любую другую шкалу тонов как их собственный контекст тонов, а не как что-то просто «неправильное» или «расстроенное» по отношению к некоторые другие предубеждения относительно тональных предпочтений. Что удивительно, так это то, как разуму требуется всего несколько секунд, чтобы приспособиться к новому контексту звуков, из-за чего член предыдущего контекста комфорта может затем стать злоумышленником. Точно так же идея контекстного предубеждения должна быть преодолена, чтобы воспринимать любую другую шкалу тонов как их собственный контекст тонов, а не как что-то просто «неправильное» или «расстроенное» по отношению к некоторые другие предубеждения относительно тональных предпочтений. Что удивительно, так это то, как разуму требуется всего несколько секунд, чтобы приспособиться к новому контексту звуков, из-за чего член предыдущего контекста комфорта может затем стать злоумышленником. Точно так же эта идея контекстуального предубеждения должна быть преодолена, чтобы воспринимать любую другую шкалу тонов как их собственный контекст тонов, а не как что-то просто "неправильное" или "расстроенное" по отношению к некоторые другие предубеждения относительно тональных предпочтений.
-----
Традиционная октаваПосле попытки втиснуть дополнительную ноту в существующую гамму из семи красивых нот ... и потерпев неудачу, я решил подойти к задаче создания новой гаммы - или контекста тонов - таким образом, который не обязательнозаботится о предубеждении утешения традиций. Я решил просто математически разделить пространство между концами «октавы» и просто посмотреть, какие тона появляются. Как упоминалось выше, я не математик или ученый-звуколог, я не могу объяснить, как делятся октавы в системе из двенадцати нот западной музыки. Все, что я мог сделать, это наблюдать, как каждая из этих двенадцати нот оказалась примерно на 105,94% больше, чем предыдущая ... что привело к шкале, которая была разделена не поровну, а логарифмически. В музыке предполагается, что это создает гамму с одинаковым темпераментом, с плавными предсказуемыми соотношениями между нотами и, таким образом, устанавливает разумный компромисс между различными методами настройки. Это звучало как хороший подход, поэтому я решил сделать то же самое со своей шкалой. Я также решил, что все мои восемь нот должны состоять из половинных нот, поэтому я разделил пространство между двумя соответствующими «октавными» тонами на шестнадцать логарифмических сегментов по 104,4273782426% между каждой восходящей нотой. Чтобы помочь людям с предубеждением к комфорту, происходящим из контекста шкалы из двенадцати нот, я решил начать и закончить свою «октаву» с установленными частотами ближайшего пианино, которое я смог найти. Зная из песни Do-Re-Mi, что "Middle C" является важной отправной точкой, я решил охватить октаву C4. Я не знаю, кто решил, что частота «Middle C» всегда должна быть ровно 261,63 Гц и почему (очевидно, это происходит от начала «A» с 440,00 Гц), но я принял это как отправную точку и разработал свою шкалу оттуда. Результаты показаны на диаграмме ниже. Чтобы помочь людям с предубеждением к комфорту, происходящим из контекста шкалы из двенадцати нот, я решил начать и закончить свою «октаву» с установленными частотами ближайшего пианино, которое я смог найти. Зная из песни Do-Re-Mi, что "Middle C" является важной отправной точкой, я решил охватить октаву C4. Я не знаю, кто решил, что частота «Middle C» всегда должна быть ровно 261,63 Гц и почему (очевидно, это происходит от начала «A» с 440,00 Гц), но я принял это как отправную точку и разработал свою шкалу оттуда. Результаты показаны на диаграмме ниже. Чтобы помочь людям с предубеждением к комфорту, происходящим из контекста шкалы из двенадцати нот, я решил начать и закончить свою «октаву» с установленными частотами ближайшего пианино, которое я смог найти. Зная из песни Do-Re-Mi, что "Middle C" является важной отправной точкой, я решил охватить октаву C4. Я не знаю, кто решил, что частота «Middle C» всегда должна быть ровно 261,63 Гц и почему (очевидно, это происходит от начала с «A» с 440,00 Гц), но я принял это как отправную точку и разработал свою шкалу оттуда. Результаты показаны на диаграмме ниже. Из песни Do-Re-Mi, что "Middle C" является важной отправной точкой, я решил охватить октаву C4. Я не знаю, кто решил, что частота «Middle C» всегда должна быть ровно 261,63 Гц и почему (очевидно, это происходит от начала «A» с 440,00 Гц), но я принял это как отправную точку и разработал свою шкалу оттуда. Результаты показаны на диаграмме ниже. Из песни Do-Re-Mi, что "Middle C" является важной отправной точкой, я решил охватить октаву C4. Я не знаю, кто решил, что частота «Middle C» всегда должна быть ровно 261,63 Гц и почему (очевидно, это происходит от начала «A» с 440,00 Гц), но я принял это как отправную точку и разработал свою шкалу оттуда. Результаты показаны на диаграмме ниже.
Я начал с существующей октавы и разделил ее шестнадцать раз вместо двенадцати. В результате получилось пять тонов, которые были точно такими же, как и стандартная октава, и несколько других были очень близки к существующим тонам. Те, которые отключены, все примерно на 1,45% меньше. Этого достаточно, чтобы заметить разницу!
Сравнение октав C4Я начал с существующей октавы и разделил ее шестнадцать раз вместо двенадцати. В результате получилось пять тонов, которые были точно такими же, как и стандартная октава, и несколько других были очень близки к существующим тонам. Те, которые отключены, все примерно на 1,45% меньше. Этого достаточно, чтобы заметить разницу!
Интересны результаты деления существующей октавы на шестнадцать вместо двенадцати. Четыре ноты (или пять, если считать конечную) были точно такой же частоты, что и существующие ноты стандартной октавы C4 (октавы, которая начинается в "Middle C" на фортепиано). К сожалению ... две из этих четырех нот не входили в число семи так называемых идеально красивых нот гаммы «До-ре-ми», но соответствовали ровным / резким нотам, сыгранным черными клавишами пианино. Так что в целом была одна треть согласия. Но в важной области красивых нот согласия было не так много. Но, опять же, согласование этих шкал не было основной целью. Сравнивая их, чтобы увидеть, какое согласие все еще имело значение, но новая шкала должна была быть только тем, что было, и не более того.
Эти восемь нот такие же гладкие и красивые, как семь нот традиционной гаммы? Это субъективный вопрос, с которым люди должны отвечать за себя, исходя из собственной эстетики и своей способности приспособить свой комфортный контекст от традиций к чему-то новому. Те, у кого тонко настроенный слух, которые всю жизнь играют музыку со стандартными семью и двенадцатью нотами традиции, возможно, никогда не смогут услышать ничего, кроме мерзости атонального беспорядка. А те, у кого нет таких предрассудков, могут услышать что-то ценное и смогут использовать эту шкалу для создания красивой музыки. В конце концов, какими бы «выключенными» или «расстроенными» некоторые из этих тонов ни казались традиционными, во многих случаях они все еще очень близки. Фактически можно сыграть музыкальное произведение, написанное в шкале из двенадцати нот, и найти приближения тех же нот в этой новой гамме. Для того, кто уже знаком с этим музыкальным произведением, оно может показаться фальшивым при воспроизведении с новой гаммой. Однако для того, кто никогда не слышал это музыкальное произведение, оно может отлично звучать с новыми тонами. Или ... основываясь на сакральной геометрии традиционной гаммы, эти новые ноты могут быть внутренне, эмпирически и объективно «уродливыми», а не «красивыми» и никуда не годиться. Не думаю, что мы узнаем об этом, пока кто-нибудь не построит инструмент, на котором можно играть на них! Или ... мы найдем того, у кого уже есть. при игре с этой новой гаммой он может звучать фальшиво. Однако для того, кто никогда не слышал это музыкальное произведение, оно может отлично звучать с новыми тонами. Или ... основываясь на сакральной геометрии традиционной гаммы, эти новые ноты могут быть внутренне, эмпирически и объективно «уродливыми», а не «красивыми» и ни к чему не подходить. Я не думаю, что мы узнаем об этом, пока кто-нибудь не построит инструмент, на котором можно играть! Или ... мы найдем того, у кого уже есть. при игре с этой новой гаммой он может звучать фальшиво. Однако для того, кто никогда не слышал это музыкальное произведение, оно может отлично звучать с новыми тонами. Или ... основываясь на сакральной геометрии традиционной гаммы, эти новые ноты могут быть внутренне, эмпирически и объективно «уродливыми», а не «красивыми» и никуда не годиться. Не думаю, что мы узнаем об этом, пока кто-нибудь не построит инструмент, на котором можно играть на них! Или ... мы найдем того, у кого уже есть. Я не думаю, что мы узнаем об этом, пока кто-нибудь не построит инструмент, на котором можно играть! Или ... мы найдем того, у кого уже есть. Я не думаю, что мы узнаем об этом, пока кто-нибудь не построит инструмент, на котором можно играть! Или ... мы найдем того, у кого уже есть.
-----
B ПурпурныйПримечания, указанные в таблице выше, могут работать. Однако после дальнейшего рассмотрения я решил начать свою шкалу с ноты B вместо ноты C, чтобы можно было найти еще лучшее выравнивание с традиционными нотами. Таким образом, как цикл нот, моя нота, которая была бы эквивалентна букве B, располагалась бы вверху или в позиции «12 часов», если бы этот цикл нот был представлен в круглой форме ... что в точности соответствует то, что я хотел сделать, и сделал.
Интересно то, как октава напоминает геометрическую прогрессию, обнаруженная в другом месте этого исследования. Еще одно место, где мы находим похожий феномен встречи концов, обеспечивающий бесконечный цикл восходящего или нисходящего повторения, - это мир цвета. Когда видимый световой спектр электромагнитной энергии изгибается в круг, так что красный и фиолетовый концы встречаются, они производят промежуточный цвет, известный как пурпурный (см. Тайну пурпурного в эссе Наслаждайтесь красивыми цветами в другом месте этого исследования. ). Пурпурный - это цвет, которого нет при линейном разделении света на радугу. Пурпурный появляется только тогда, когда эта в остальном линейная последовательность цветов либо накладывается рядом с другим линейным спектром, либо изгибается так, что ее собственные концы встречаются. Создавая этот промежуточный цвет, в противном случае линейная прогрессия превращается в бесконечную круговую прогрессию. Таким образом, пурпурный становится эквивалентным Точке, которая также является Сферой, или ноте C, переходящей в другую C. Итак, включив пурпурный в нашу последовательность цветов, мы устанавливаем три бесконечных постепенных прогрессии: цвет, музыка и геометрия. Могут ли они быть объединены в одно целое?
Многие люди ассоциируют цвета радуги с музыкой. Тем не менее, большую часть времени они связывают семь нот традиционной гаммы с семью цветами света, как определил сэр Исаак Ньютон ..., пропуская жизненно важный цвет пурпурный как связь между красным и фиолетовым, которая делает это в остальном линейным. спектр должен быть цикличным. Где пурпурный цвет между красным и фиолетовым на этих шкалах? Его удобно проигнорировать, чтобы сопоставить семь цветов с семью нотами. Семерка всегда была популярным числом, которым люди одержимы; семь нот, семь цветов, семь чакр, семь планет и т. д. Но это изучение нумерологии, цвета и музыки не зацикливается на числе семь ... мы зацикливаемся на числе девять! Создав музыкальную гамму с восемью нотами и девятой, совпадающей по фазе, или так же, как первое, только увеличенное или уменьшенное, мы можем приравнять музыкальные ноты к девяти числам нумерологии и превратить октаву звука в истинный цикл «точка-сфера» ... показывая жизненный цикл этап связывания, который позволяет одному циклу повторяться на той же местности в ее повышенном или пониженном состоянии. И когда мы применяем эту идею жизненно важного связующего звена к миру цвета, мы видим, что это какВ цикле на самом деле цветов восемь, а не семь! Фактически ... как единая линейная последовательность расщепления света на цвета, на самом деле существует множество возможных цветов, которые мы могли бы обозначить. Можно сказать, что их семь или больше семи. Но если мы не признаем существование пурпурного как связующего цвета, эта линейная последовательность цветов - сколько бы мы ни назвали - не станет круговой или циклической ... она останется линейной и конечной. Пурпурный - вот что заставляет его цикл.
Если ... в моем стремлении найти инструмент, способный играть на этих тонах, я смогу изготовить любой инструмент, похожий на пианино, я не буду делать клавиши черными и белыми ... Я раскрашу их соответствующим цветом и обозначьте их соответствующими номерами - в соответствии с тем, как они будут выстраиваться вместе в круговой таблице цветов и заметок. Серьезным музыкантам инструмент, созданный с такой цветовой и числовой схемой, может показаться юным или чрезмерно ярким, но я бы приветствовал это как празднование брака между этими тремя циклическими системами и того, как каждая из них усиливает выражение другой.
-----
B для двоичногоПосле того, как я задумал такое круговое представление цветов, геометрии и музыки, я подумал, что было бы неплохо, если бы моя шкала была выровнена с симметричным рисунком 12-тонной хроматической шкалы, когда она тоже была расположена по кругу. В таком расположении я видел черную ключевую ноту G # / Ab как вершину или точку пентакулярного расположения черных клавиш, и впоследствии снова скорректировал свои ноты, чтобы они начинались и заканчивались в этой критической точке вместо C или B. Я сделал это ради симметрии, чтобы было легче увидеть сравнение между системами, особенно при рассмотрении интервалов между нотами, которые считаются гармоничными в трезвучиях и аккордах. Однако ... когда я начал изучать тему трезвучий, аккордов и гармоник, появилось нечто, что снова изменило мое направление!
Поскольку моя шкала делит октаву на 16 или 8 нот, она по сути является двоичной, поскольку 16 и 8 являются частью двоичной последовательности чисел, где каждое число в двоичной последовательности вдвое или в два раза больше своего соседа (1, 2, 4 , 8, 16, 32, 64, 128, 256 и т. Д.) Это вид числового мышления, используемый в цифровом мире компьютеров, чтобы говорить на языке Вселенной. Это очень простой, обычный и легкий для понимания шаблон. Нам нравятся простые, обычные, простые для понимания универсальные закономерности в изучении космологии и закономерностей природы. Помня об этом, я начал искать другие способы, которыми двоичная последовательность могла бы играть роль в формировании музыкального строя.
В более ранних версиях моих 16 заметок я беспокоился о том, насколько мои заметки были близки или далеки от традиционных заметок 12TET. Я хотел, чтобы мои ноты были доступны всем, и хотел, чтобы их можно было использовать даже для воспроизведения существующей музыки. Но в конечном итоге не было никакого способа приблизить банкноты к традициям, более близким к 1,45%. Я мог бы сделать некоторых ближе, но это только отдаляло бы других. Я попытался отказаться от логарифмической схемы и настроить все мои близкие ноты, чтобы они были ближе. Но из-за неравномерного темперамента звучание нот звучало плохо. В конце концов, я отказался от всякого интереса к тому, чтобы мои заметки вообще соответствовали традиции, и начал искать шкалу нот, которая звучала бы хорошо и, если возможно, имела некоторую связь с двоичной последовательностью.
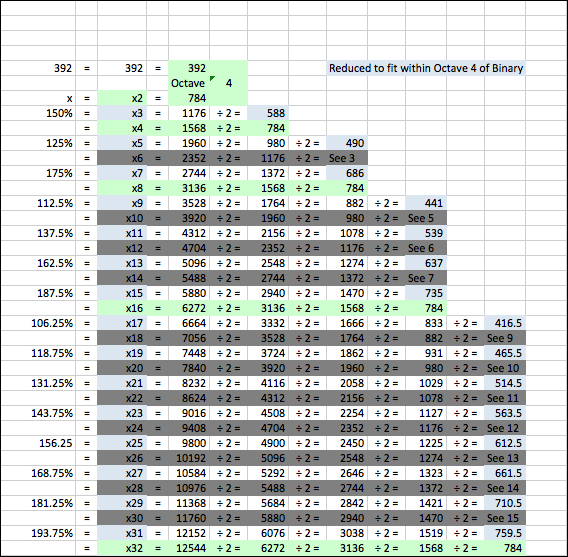
Попутно у меня появилось желание отойти от иррациональных чисел, которые появляются, когда прямая и строгая логарифмическая прогрессия применяется к любой начальной частоте. Поэтому я искал последовательность паттернов, в которой для частот использовались только целые числа, а для интервала между частотами - только целые числа. Мне удавалось это делать несколько раз, но, к сожалению, каждый раз последовательность работала только для одной октавы. Это означает, что когда последовательность пересекает этот октавный «порог» и следующая частота должна быть в два раза больше, чем в предыдущей октаве, переход от последней частоты предыдущей октавы к первой частоте следующей октавы не был плавным. Иногда был большой скачок, иногда был отрицательный скачок. Я столкнулся с этой проблемой с нескольких попыток. В процессе поиска я приобрел приложение для осциллографа и начал поиск частот стоячей волны. Я подумал, что было бы круто создать музыкальную шкалу на стоячих волнах. Я сделал октаву стоячей волны, которая начиналась с частот от 344 Гц до 688 Гц (округленные вниз от 344,4 до 688,8, чтобы получить целые числа). Это почти сработало. Я попытался начать с хорошего круглого числа, например, от 400 до 800. Это почти сработало, но не совсем. На приведенной ниже диаграмме показано, как попытки перейти от идеи стоячей волны к уменьшению «скачка» между октавами и попытки уменьшить «скачок» между октавами с идеи 400, чтобы уменьшить «скачок» между октавами, привели меня к единственному уединенному решению ... очевидно, ЕДИНСТВЕННОЕ возможное решение для шкалы, требующей целых частот и целочисленных интервалов! Из-за этого чудесного откровения, и
Я попробовал шкалу стоячей волны с округленными целыми числами. Я попытался начать с пентакулярной пиковой частоты округленного G # / Ab на уровне 416. Я попробовал хорошее круглое число, например, 400. «Переход» между октавами был не лучшим. Пока я не переместил один вверх, а другой вниз, чтобы найти эту идеальную последовательность целых чисел частот и целых чисел интервалов между частотами. Тот факт, что интервалы заканчивались 16 шагами с интервалом 32, заставил меня рассматривать это как космически вдохновленную «двоичную» шкалу!Итак, после многих тупиков я нашел его (эврика!). И ... к счастью ... это очень «двоичный» паттерн. Однако двоичную природу шкалы нельзя увидеть только при отображении нот, потому что именно в этой базовой структуре возникла каждая нота. Но это круто, как это работает. Вот еще один график, показывающий, насколько "двоична" эта шкала:
Эта шкала частоты целых чисел / интервалов целых чисел очень «двоична» по своей базовой структуре, создавая шкалу, которая не является точно логарифмической, но очень близкой ... квазилогарифмической. Целочисленные частоты звучат лучше? Я не знаю. Но это круто! Следует отметить, что частоты и интервалы ниже отметки 392 Гц не являются целыми числами. Но ... все дробные количества, которые они используют, основаны на очень двоичной природе разделения целого на 1/2, 1/4, 1/8, 1/16 и т. Д., Что само по себе соответствует двоичной схеме 2, 4, 8, 16 и т. Д. Таким образом, даже в виде дробей мы остаемся двоичными по образцу, так же как и в степени увеличения от одного интервала к другому; увеличиваясь на 1 в одной октаве, затем на 2 в следующей октаве, затем на 4 в следующей, затем на 8 и т.д.Конечным результатом является не идеально логарифмическое увеличение нот, а вместо этого серия увеличений целых чисел, которые приводят к серии частот целых чисел ... пока не дойдут до более низких нот, где все дроби равны 1/2, 1/4, 1/8, 1/16 ... который сам по себе является двоичным. И когда каждая серия интервалов целых чисел достигает конца своей октавы, она заканчивается двоичным числом. И поскольку первый интервал этой октавы удваивается в следующей октаве, переход от последнего интервала к первому интервалу плавный (30, 31, 32-34), где следующая октава увеличивается в два раза в каждом интервале ( 34, 36, 38 и т. Д.). Итак ... не * идеально * логарифмически, но достаточно близко, чтобы все работало. Да и сами ноты звучат неплохо. По-прежнему сложно сказать, из-за того, как наши уши натренированы на 7 вместо 8, но они определенно звучат лучше, чем любой предыдущий прогресс. И я считаю, что сформированные ими гармонические трезвучия вполне адекватны. Они могут быть недостаточно хороши для экспертов, но я думаю, что «двоичный» характер этого решения делает его единственной разумной точкой опоры для этого эксперимента.
Итак ... посмотрим, что вы можете сделать с ЭТИМИ нотами ... Вот ссылка на другую страницу, где вы можете играть эти ноты!
Некоторые из этих нот до сих пор соответствуют традиции. Это неизбежно при наложении системы из 16 нот на систему из 12 нот. Но имейте в виду, что здесь не делается попыток дублировать традиционные записи. Так что, вероятно, будет нецелесообразно пытаться играть существующую музыку с этими нотами. Придумайте что-нибудь совершенно неслыханное и посмотрите, понравится ли нам это.
Вот еще один рисунок, показывающий 96 из этих космически вдохновленных нот по спирали:
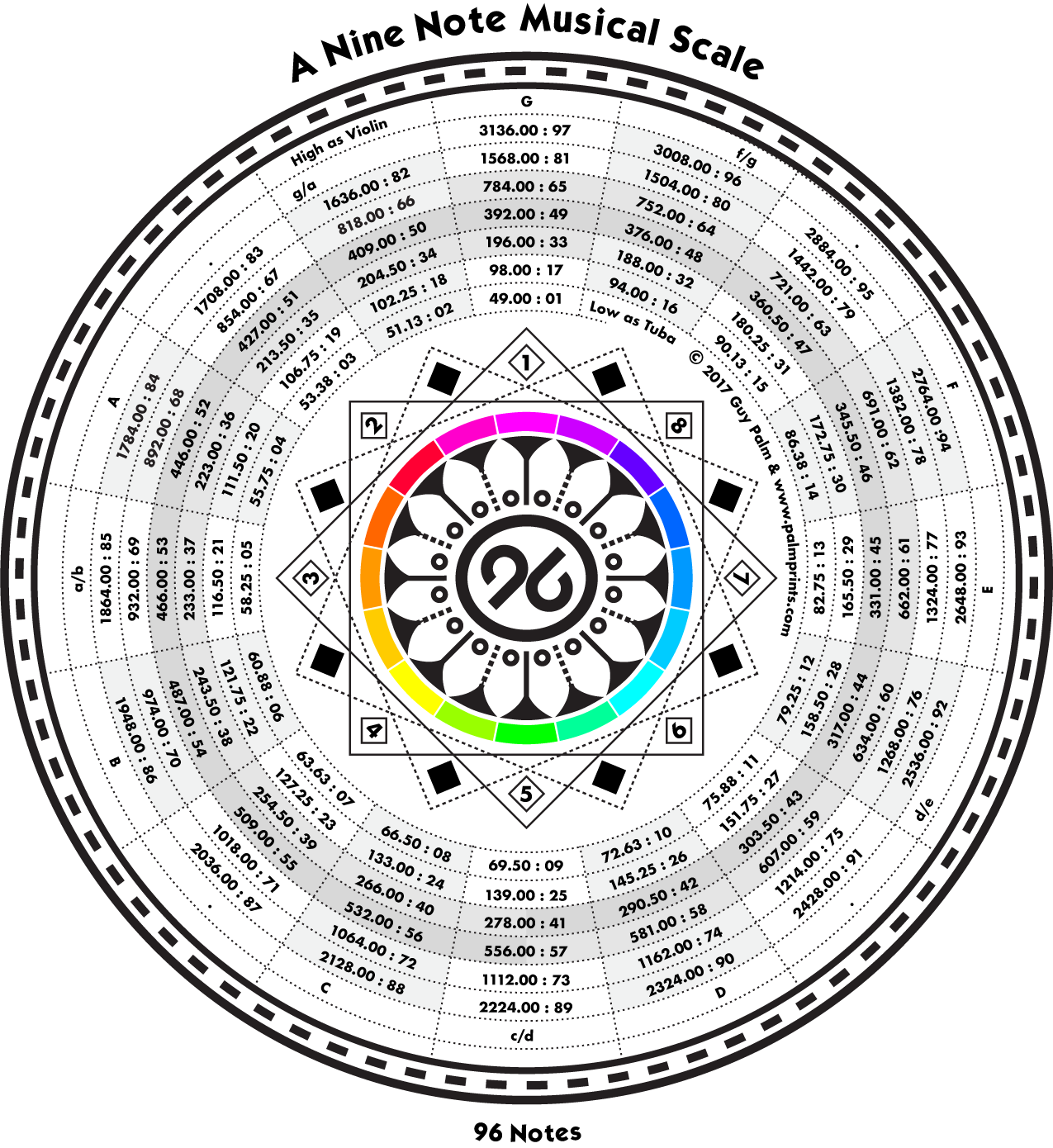Вот 96 вдохновленных космосом, двоичных нот, которые можно использовать при воспроизведении музыки! Они не так идеально сочетаются с традиционными нотами 12TET, как предыдущие аранжировки. Но они совпадают с традиционной нотой G, поэтому можно провести некоторые сравнения с точки зрения общности. Поскольку он сочетается с G, а не с G # / Ab, ему также не хватает симметрии традиционной шкалы 12TET - необходимая жертва для такого крутого расположения нот!Эти ноты не так идеально сочетаются с традиционными нотами 12TET, как предыдущие аранжировки. Но они совпадают с традиционной нотой G, поэтому можно провести некоторые сравнения с точки зрения общности. Поскольку он сочетается с G, а не с G # / Ab, ему также не хватает пентакулярной симметрии традиционной гаммы 12TET - необходимая жертва для такого крутого расположения нот!
-----
Гармоники двоичны!Создав классную серию заметок, я решил исследовать тему гармоник. Еще одна тема, о которой я мало знаю! Но исследования приводят меня к более интересным встречам с бинарными паттернами.
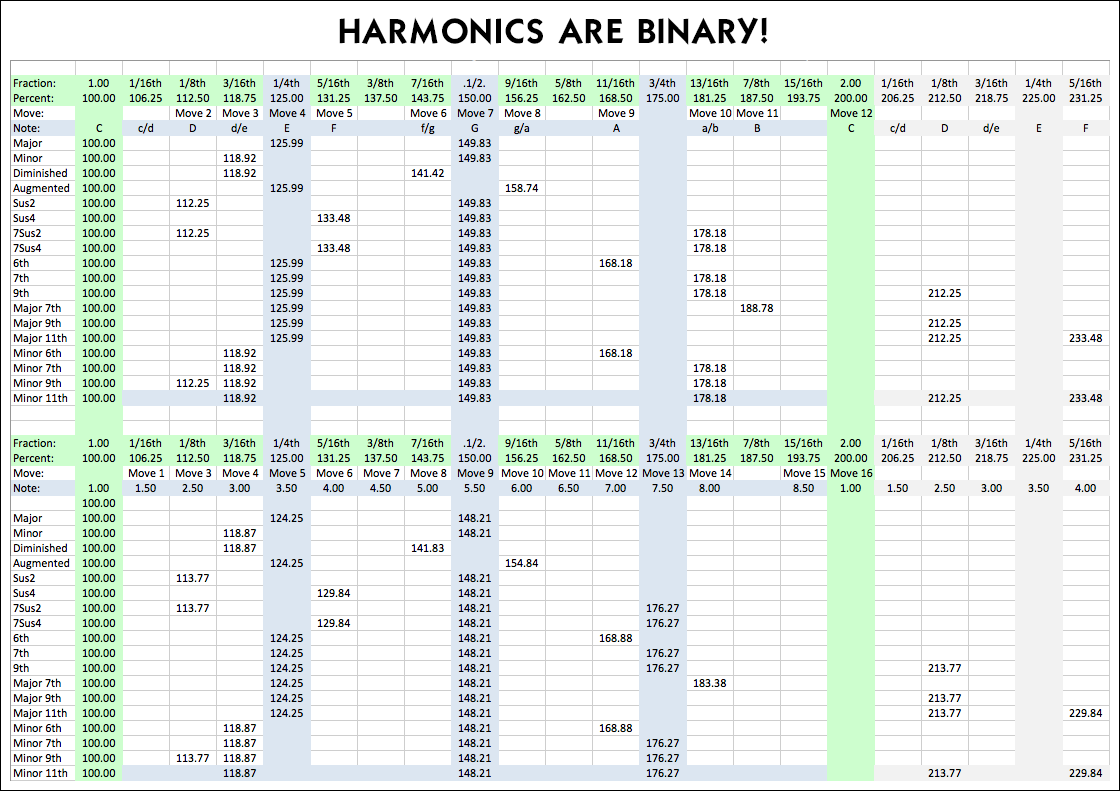
Я считаю, что моя двоичная шкала довольно крутая, потому что она использует двоичную последовательность (1, 2, 4, 8, 16, 32, 64 и т. Д.) Для определения своей формы и создания заметок. Я не знаю, правильно ли я понимаю гармоники или нет, но я придумал эту диаграмму, в которой я расширил умножения, которые используются для создания отношений между
нотами. Выяснилось много интересного:
Когда вы удваиваете ноту, вы получаете гармонию из-за явления октавы. Когда вы умножаете 4, 8 или 16 раз, вы получаете ту же гармонию. Когда вы умножаетесь в 3 раза, вы получаете другую гармонию. В этом случае нота получается гармоничной, потому что она ровно на 150% больше основного тона. Когда вы умножаете на 5, происходит то же самое, за исключением того, что теперь нота становится гармоничной, потому что она ровно на 125% больше основной ноты. Когда вы умножаете на 6, вы дублируете ту же гармонию, что и умножение на 3. Когда вы умножаете на 7, нота становится гармоничной, потому что она ровно на 175% больше, чем основной тон. Все эти проценты соответствуют обычным долям целого; 125% - это 1/4, 150% - 1/2, а 175% - 3/4 ... что по сути то же самое, что 1/4, в зависимости от того, как вы смотрите на вещи. Последующие умножения показывают, что все уникальные частоты имеют проценты, равные двоичным дробным числам! 112,5% - это 1/16. Форма гармоник бинарная. И когда повторяющиеся частоты удаляются или затемняются серым цветом, мы видим двоичный образец в количестве уникальных частот, существующих между каждой дублирующейся октавной нотой; от 2 до 4 раз есть одна уникальная частота. От 4 до 8 раз - 2. От 8 до 16 раз - 4. От 16 до 32 раз - 8 уникальных частот. Этот образец продолжается. Гармоники бинарны! мы видим двоичный паттерн в количестве уникальных частот, существующих между каждой повторяющейся октавной нотой; от 2 до 4 раз есть одна уникальная частота. От 4 до 8 раз - 2. От 8 до 16 раз - 4. От 16 до 32 раз - 8 уникальных частот. Этот образец продолжается. Гармоники бинарны! мы видим двоичный образец в количестве уникальных частот, существующих между каждой дублирующейся октавной нотой; от 2 до 4 раз есть одна уникальная частота. От 4 до 8 раз - 2. От 8 до 16 раз - 4. От 16 до 32 раз - 8 уникальных частот. Этот образец продолжается. Гармоники бинарны!Во-первых ... несмотря на то, что 12-ступенчатая шкала - это неплохо, я думаю, что основание шкалы на идее удвоения имеет свой шарм. Октава важна для звука и музыки. Вы получаете октаву удвоением. Поэтому шкала, в которой для создания нот используется идея удвоения (1, 2, 4, 8, 16, 32, 64 и т. Д.), Кажется подходящей. Так что было интересно увидеть, как «уникальные» ноты этой гармонической последовательности (окрашенные в синий цвет) попали в группы по 1, 2, 4, 8 и 16! (если вы видите серую строку, это означает, что эта последовательность чисел уже была установлена в предыдущей строке). Также было интересно увидеть, как процент увеличения от основной частоты к каждой уникальной частоте выражается в виде дробной двоичной величины, а не в виде некоторого иррационального числа.
Имея в руках этот шаблон, я сравнил уникальные числа из моей таблицы по вычисленным гармоникам с моей текущей двоичной шкалой целых чисел ... и со шкалой 12 TET, как показано на диаграмме ниже:
На этой диаграмме видно, что некоторые из моих нот немного дальше от «идеального», чем мне бы хотелось, но многие из моих нот довольно близки к синей гармонической ноте того или иного вида. Мне пришлось перейти к x57, чтобы получить число, близкое к 12-тоновому F, и к x43, чтобы получить приличный C. То же самое и для моей шкалы. Но в целом моя целая числовая шкала и целая числовая шкала интервалов не так уж далеки от «идеальной» в представлении идеальных гармонических нот. То есть ... если я правильно на это смотрю! В моей шкале большинство моих нот не превышают 5 Гц. Шкала 12 тонов могла бы быть лучше, только с парой, которая находится далеко, например, B и f / g. Но то, что мой масштаб настолько близок, отрадно.
-----
C Что я имею в видуКак уже говорилось, не предпринимается никаких попыток дублировать 12-тоновые ноты с помощью этой двоичной шкалы. Но сравнения неизбежны, поэтому я пошел дальше, чтобы сравнить, как моя гамма достигает гармоничного смешения нот как трезвучий и аккордов, по сравнению с традиционной 12-тонной системой.
Когда гармонические частоты были рассчитаны (и уменьшены для соответствия одной октаве), первой гармоникой была частота октавы, в два раза превышающая корень, или «корень x 2», или «200% корня». Последующие гармоники продолжались оттуда. После этого мы должны были умножить на 3. Это дало нам частоту, равную 150% от корня. Следующая гармоника (x4) повторяет ту же частоту, что и x2. Следующая уникальная частота появилась, когда мы умножили на 5. Мы получили частоту, которая составила 125% от корня. Далее умножение на 6 повторяет ту же частоту, что и x3. Следующая уникальная частота появилась, когда мы умножили на 7. Мы получили частоту, которая составила 175% от корня. Частоты после этого все имели проценты увеличения, которые имели двоичные дроби!
Когда мы смотрим на основную триаду по шкале 12TET, начиная с G, она просит нас объединить G с B и D, чтобы получить приятную комбинацию. Нота B составляет чуть больше 125% от G, а D почти точно составляет 150% от G. Звучит ли эта комбинация хорошо, потому что эти ноты близки к этой идеальной гармонической ассоциации 125% и 150%? Если так ... гармоники двоичны! Одна гармоника удваивается. Следующее - 1/2 от этого. Следующее - 1/2 от этой 1/2 или 1/4. Даже малая триада просит нас переместить эту вторую ноту на A # Bb, которая находится почти ровно на 3/16 (118,75% или 1,1875) от корня G.
Можно подумать, что было бы идеально создать шкалу, которая точно соответствует этим идеальным двоичным гармоникам. Было бы. Я пробовал это ... с 16 нотами ... по одной на каждую 1/16 шага. Звучало прекрасно. Гармоники были. Однако одна проблема ... каждый интервал был одинаковым, поэтому ... как указано выше, когда вы достигаете этой октавной частоты, которая в два раза больше корня, и начинаете другую октаву, вам нужно удваивать каждую последующую частоту ... и каждый интервал ... это означает, что есть заметный скачок между меньшими интервалами первой октавы и большими интервалами следующей. Урок ... что у вас вроде естьбыть логарифмическим по интервалу частот. Или, как в моей шкале «квазилогарифмическая», так что последний интервал одной октавы переходит к первому интервалу следующей октавы с небольшим «скачком» или без него.
Итак ... если эти двоичные дробные величины важны для гармонии, вопрос при оценке шкалы может быть сосредоточен вокруг того, какая логарифмическая шкала ближе всего подходит к важным двоичным отметкам гармоник. Моя «квазилогарифмическая» шкала «целое число / интервал целого числа» требует небольшого скачка, который нужно учитывать. Но в целом он достигает некоторых важных частот примерно с такой же точностью, как шкала 12TET. Мы оба примерно на одинаковую сумму от идеальной банкноты в 125%. 12TET очень близок к 150%, а мне немного не хватает. Но тогда ... Я намного ближе к отметке 175%, если кому-то это нужно! И мы оба почти точно достигли отметки 3/16.
Вот диаграмма, чтобы лучше понять, как ноты выглядят как 1/2, 1/4, 1/8 и 1/16 корня / октавы или двоичные!
Эта диаграмма показывает, как две логарифмические шкалы совпадают с не очень логарифмической схемой двоичных дробей.На этой диаграмме мы видим, что шкала 12TET лучше справляется с достижением идеальных частот в начале (верхний левый квадрант). Но ... между моими нотами 3 и 7 у меня семь нот; по одному на каждую "идеальную" ноту, тогда как в 12TET их всего пять. Мои все немного далеки от идеала, но, по крайней мере, я следую идеалу с примечанием для каждого. Собственно с моей заметки 2.5 на 7.5 у меня по одному на каждую. Только в самом начале и в самом конце я не придерживаюсь идеала. Что не так важно, потому что эти ноты слишком близки к основной частоте, чтобы в любом случае добиться гармонии. Вам действительно нужно пройти эту точку на 3/16, прежде чем все начнет звучать близко к гармоническому. И выход за пределы этой отметки 175% / 3/4 также становится сомнительным. Итак, в целом моя шкала довольно точно соответствует бинарному гармоническому идеалу! Все идет нормально.
-----
C для аккордовНаблюдая за тем, как моя квазилогарифмическая шкала из 16 нот покрывает нелогарифмические 16 сегментов целого при делении на 1/2, 1/4, 1/8 1/16 лучше, чем традиционная 12-тональная система, я решил исследовать насколько близка эта гамма к созданию реальных трезвучий и аккордов. Это привело к еще одному интересному графику:
Поскольку моя шкала не совсем логарифмическая, но имеет этот крошечный скачок между октавами, процент увеличения от основного числа до гармонической ноты не всегда одинаков. Он может отличаться на другой процентный пункт или около того, в зависимости от того, пересекает ли триада этот октавный порог или нет. Строго логарифмическая прогрессия не будет иметь никакого «порога», который нужно пересечь, и процент увеличения будет одинаковым для любого корня. Но разброс моей шкалы минимален (или, судя по всему, на основании экспериментов со звуковыми файлами). Так что это в основном мои проценты увеличения по сравнению с процентом увеличения, необходимым для получения трезвучий и аккордов в системе 12TET.
Идея этой диаграммы состоит в том, что гармоники бинарны. Поэтому я разделил октаву на 16-е и рассчитал процент увеличения, необходимый для точного попадания каждой 16-й доли. Затем ... нанес на карту положение каждого типа аккорда, который я нашел, на большой таблице аккордов фортепиано. В таблице отображено 216 изображений аккордов (по 12 изображений для каждого из 18 типов аккордов). Но на самом деле картина одинакова для всех 12 нот. Этот образец можно увидеть по-разному. Я решил показать это как процент увеличения от основной ноты, чтобы увидеть, насколько близко этот процент приближается к предполагаемому идеалу двоичных приращений.
Как говорилось ранее, моя шкала немного дотягивает до критической отметки 1/2 или 150%. Но я думаю, что он все еще достаточно близок для работы (даже если он варьируется, чтобы быть немного дальше). И ... моя заметка 7.5 намного ближе к другой критической точке - отметке 3/4 или 175%. В общем, на этой диаграмме можно увидеть, что образцы аккордов группируются вокруг этих трех основных отметок: 1/4 или 125%, 1/2 или 150% и 3/4 или 175%. В этом есть смысл, если вы хотите сделать что-то гармоничное, вы комбинируете это с таким же рисунком ... только двойным, 1/2, 1/4 или 3/4. И если вы хотите сделать несколько интересных исключений, вы все равно не уходите слишком далеко от этих критических точек.
Итак, у меня есть двоичная шкала, потому что в ней 8 или 16 нот. И потому, что его основная структура использует двоичные приращения для определения этих 16 частот и интервалов. И потому, что в нем больше нот, соответствующих двоичной дробной структуре гармоник! Но ... как это звучит? Зайдите ЗДЕСЬ и поэкспериментируйте с некоторыми звуковыми файлами. Или сделайте инструмент, который может играть на этих нотах! А потом ... сделай мне одну !!
Вот еще одна мандала, которая показывает, что эта новая двоичная шкала совмещена с частотами 12-тональной системы. К сожалению, это не совпадает с высшей точкой пентакля симметрии, существующей в 12-тональной системе. Эта мандала показывает ноты, расположенные на одинаковом расстоянии, и критические двоичные дробные точки гармонии логарифмически, а не наоборот (как показано на предыдущей диаграмме). Важно понимать, что середина круга - это не то же самое, что и середина частот. Используйте это, чтобы найти различные формы гармонии.Все слова и изображения Copyright © 1980-2016, Гай Палм
Назад к деталям || Вернуться к книге | Вернуться к Таро | Главная | Карта сайта
Изучение Таро Использование Таро
Узоры Структура Резюме Философия заявка
Читать книгу! ...
Содержание удалено:
Купить книги
- Элементы ...
Времена года ...
Содержание удалено:
Купить книги
Ключевые модели ...
Ключевые диаграммы ...
Таблицы колод ...
Расположение палубы ...
Мандалы ...
Стихи ...
Искусство ...
Квинтаграммы ...
ХРАНИТЬ! МАГАЗИН! КУПИТЬ! ...
Содержание удалено:
Купить книги
Таро на костях ...
Мандала удачи ...
Мудры ...
Мантры ...
Музыка ...
*****************************************************************************************************************Если вы хотите обсудить идеи, найденные на этом сайте, перейдите по адресу :
http://groups.yahoo.com/group/TarotAlternative/Yahoo Groups Shutdown
Yahoo Groups officially shut down on December 15. This change will not impact your Yahoo Mail account or any other Yahoo products, including Yahoo News, Yahoo Finance, Yahoo Sports and Yahoo Entertainment. Please visit Yahoo.com to access Yahoo Mail and our other properties.
Back in October we notified all Yahoo Group members via email and the website that Yahoo Groups will be shut down on December 15. Here is a link to the FAQ that includes alternative providers and information on how this impacts your group content.
************************************************************************************************************Эволюция музыкиЯ попробовал шкалу стоячей волны с округленными целыми числами. Я попытался начать с пентакулярной пиковой частоты округленного G # / Ab на уровне 416. Я попробовал хорошее круглое число, например, 400. «Переход» между октавами был не лучшим. Пока я не переместил один вверх, а другой вниз, чтобы найти эту идеальную последовательность целых чисел частот и целых чисел интервалов между частотами. Тот факт, что интервалы заканчивались 16 шагами с интервалом 32, заставил меня рассматривать это как космически вдохновленную «двоичную» шкалу!
Итак, после многих тупиков я нашел его (эврика!). И ... к счастью ... это очень «двоичный» паттерн. Однако двоичную природу шкалы нельзя увидеть только при отображении нот, потому что именно в этой базовой структуре возникла каждая нота. Но это круто, как это работает. Вот еще один график, показывающий, насколько "двоична" эта шкала:
Базовая структураЭта шкала частоты целых чисел / интервалов целых чисел очень «двоична» по своей базовой структуре, создавая шкалу, которая не является точно логарифмической, но очень близкой ... квазилогарифмической. Целочисленные частоты звучат лучше? Я не знаю. Но это круто! Следует отметить, что частоты и интервалы ниже отметки 392 Гц не являются целыми числами. Но ... все дробные количества, которые они используют, основаны на очень двоичной природе разделения целого на 1/2, 1/4, 1/8, 1/16 и т. Д., Что само по себе соответствует двоичной схеме 2, 4, 8, 16 и т. Д. Таким образом, даже в виде дробей мы остаемся двоичными по образцу, так же как и в степени увеличения от одного интервала к другому; увеличиваясь на 1 в одной октаве, затем на 2 в следующей октаве, затем на 4 в следующей, затем на 8 и т.д.
Конечным результатом является не идеально логарифмическое увеличение нот, а вместо этого серия увеличений целых чисел, которые приводят к серии частот целых чисел ... пока не дойдут до более низких нот, где все дроби равны 1/2, 1/4, 1/8, 1/16 ... который сам по себе является двоичным. И когда каждая серия интервалов целых чисел достигает конца своей октавы, она заканчивается двоичным числом. И поскольку первый интервал этой октавы удваивается в следующей октаве, переход от последнего интервала к первому интервалу плавный (30, 31, 32-34), где следующая октава увеличивается в два раза в каждом интервале ( 34, 36, 38 и т. Д.). Итак ... не * идеально * логарифмически, но достаточно близко, чтобы все работало. Да и сами ноты звучат неплохо. По-прежнему сложно сказать, из-за того, как наши уши натренированы на 7 вместо 8, но они определенно звучат лучше, чем любой предыдущий прогресс. И я считаю, что сформированные ими гармонические трезвучия вполне адекватны. Они могут быть недостаточно хороши для экспертов, но я думаю, что «двоичный» характер этого решения делает его единственной разумной точкой опоры для этого эксперимента.
Итак ... посмотрим, что вы можете сделать с ЭТИМИ нотами ... Вот ссылка на другую страницу, где вы можете играть эти ноты!
Некоторые из этих нот до сих пор соответствуют традиции. Это неизбежно при наложении системы из 16 нот на систему из 12 нот. Но имейте в виду, что здесь не делается попыток дублировать традиционные записи. Так что, вероятно, будет нецелесообразно пытаться играть существующую музыку с этими нотами. Придумайте что-нибудь совершенно неслыханное и посмотрите, понравится ли нам это.
Вот еще один рисунок, показывающий 96 из этих космически вдохновленных нот по спирали:
Спираль двоичной шкалыВот 96 вдохновленных космосом, двоичных нот, которые можно использовать при воспроизведении музыки! Они не так идеально сочетаются с традиционными нотами 12TET, как предыдущие аранжировки. Но они совпадают с традиционной нотой G, поэтому можно провести некоторые сравнения с точки зрения общности. Поскольку он сочетается с G, а не с G # / Ab, ему также не хватает симметрии традиционной шкалы 12TET - необходимая жертва для такого крутого расположения нот!
Эти ноты не так идеально сочетаются с традиционными нотами 12TET, как предыдущие аранжировки. Но они совпадают с традиционной нотой G, поэтому можно провести некоторые сравнения с точки зрения общности. Поскольку он сочетается с G, а не с G # / Ab, ему также не хватает пентакулярной симметрии традиционной гаммы 12TET - необходимая жертва для такого крутого расположения нот!
-----
Гармоники двоичны!Создав классную серию заметок, я решил исследовать тему гармоник. Еще одна тема, о которой я мало знаю! Но исследования приводят меня к более интересным встречам с бинарными паттернами.
Я считаю, что моя двоичная шкала довольно крутая, потому что она использует двоичную последовательность (1, 2, 4, 8, 16, 32, 64 и т. Д.) Для определения своей формы и создания заметок. Я не знаю, правильно ли я понимаю гармоники или нет, но я придумал эту диаграмму, в которой я расширил умножения, которые используются для создания отношений между нотами. Выяснилось много интересного:
Калькулятор гармоникКогда вы удваиваете ноту, вы получаете гармонию из-за явления октавы. Когда вы умножаете 4, 8 или 16 раз, вы получаете ту же гармонию. Когда вы умножаетесь в 3 раза, вы получаете другую гармонию. В этом случае нота получается гармоничной, потому что она ровно на 150% больше основного тона. Когда вы умножаете на 5, происходит то же самое, за исключением того, что теперь нота становится гармоничной, потому что она ровно на 125% больше основной ноты. Когда вы умножаете на 6, вы дублируете ту же гармонию, что и умножение на 3. Когда вы умножаете на 7, нота становится гармоничной, потому что она ровно на 175% больше, чем основной тон. Все эти проценты соответствуют обычным долям целого; 125% - это 1/4, 150% - 1/2, а 175% - 3/4 ... что по сути то же самое, что 1/4, в зависимости от того, как вы смотрите на вещи. Последующие умножения показывают, что все уникальные частоты имеют проценты, равные двоичным дробным числам! 112,5% - это 1/16. Форма гармоник бинарная. И когда повторяющиеся частоты удаляются или затемняются серым цветом, мы видим двоичный образец в количестве уникальных частот, существующих между каждой дублирующейся октавной нотой; от 2 до 4 раз есть одна уникальная частота. От 4 до 8 раз - 2. От 8 до 16 раз - 4. От 16 до 32 раз - 8 уникальных частот. Этот образец продолжается. Гармоники бинарны! мы видим двоичный паттерн в количестве уникальных частот, существующих между каждой повторяющейся октавной нотой; от 2 до 4 раз есть одна уникальная частота. От 4 до 8 раз - 2. От 8 до 16 раз - 4. От 16 до 32 раз - 8 уникальных частот. Этот образец продолжается. Гармоники бинарны! мы видим двоичный образец в количестве уникальных частот, существующих между каждой дублирующейся октавной нотой; от 2 до 4 раз есть одна уникальная частота. От 4 до 8 раз - 2. От 8 до 16 раз - 4. От 16 до 32 раз - 8 уникальных частот. Этот образец продолжается. Гармоники бинарны!
Во-первых ... несмотря на то, что 12-ступенчатая шкала - это неплохо, я думаю, что основание шкалы на идее удвоения имеет свой шарм. Октава важна для звука и музыки. Вы получаете октаву удвоением. Поэтому шкала, в которой для создания нот используется идея удвоения (1, 2, 4, 8, 16, 32, 64 и т. Д.), Кажется подходящей. Так что было интересно увидеть, как «уникальные» ноты этой гармонической последовательности (окрашенные в синий цвет) попали в группы по 1, 2, 4, 8 и 16! (если вы видите серую строку, это означает, что эта последовательность чисел уже была установлена в предыдущей строке). Также было интересно увидеть, как процент увеличения от основной частоты к каждой уникальной частоте выражается в виде дробной двоичной величины, а не в виде некоторого иррационального числа.
Имея в руках этот шаблон, я сравнил уникальные числа из моей таблицы по вычисленным гармоникам с моей текущей двоичной шкалой целых чисел ... и со шкалой 12 TET, как показано на диаграмме ниже:
Гармоники в процентахНа этой диаграмме видно, что некоторые из моих нот немного дальше от «идеального», чем мне бы хотелось, но многие из моих нот довольно близки к синей гармонической ноте того или иного вида. Мне пришлось перейти к x57, чтобы получить число, близкое к 12-тоновому F, и к x43, чтобы получить приличный C. То же самое и для моей шкалы. Но в целом моя целая числовая шкала и целая числовая шкала интервалов не так уж далеки от «идеальной» в представлении идеальных гармонических нот. То есть ... если я правильно на это смотрю! В моей шкале большинство моих нот не превышают 5 Гц. Шкала 12 тонов могла бы быть лучше, только с парой, которая находится далеко, например, B и f / g. Но то, что мой масштаб настолько близок, отрадно.
-----
C Что я имею в видуКак уже говорилось, не предпринимается никаких попыток дублировать 12-тоновые ноты с помощью этой двоичной шкалы. Но сравнения неизбежны, поэтому я пошел дальше, чтобы сравнить, как моя гамма достигает гармоничного смешения нот как трезвучий и аккордов, по сравнению с традиционной 12-тонной системой.
Когда гармонические частоты были рассчитаны (и уменьшены для соответствия одной октаве), первой гармоникой была частота октавы, в два раза превышающая корень, или «корень x 2», или «200% корня». Последующие гармоники продолжались оттуда. После этого мы должны были умножить на 3. Это дало нам частоту, равную 150% от корня. Следующая гармоника (x4) повторяет ту же частоту, что и x2. Следующая уникальная частота появилась, когда мы умножили на 5. Мы получили частоту, которая составила 125% от корня. Далее умножение на 6 повторяет ту же частоту, что и x3. Следующая уникальная частота появилась, когда мы умножили на 7. Мы получили частоту, которая составила 175% от корня. Частоты после этого все имели проценты увеличения, которые имели двоичные дроби!
Когда мы смотрим на основную триаду по шкале 12TET, начиная с G, она просит нас объединить G с B и D, чтобы получить приятную комбинацию. Нота B составляет чуть больше 125% от G, а D почти точно составляет 150% от G. Звучит ли эта комбинация хорошо, потому что эти ноты близки к этой идеальной гармонической ассоциации 125% и 150%? Если так ... гармоники двоичны! Одна гармоника удваивается. Следующее - 1/2 от этого. Следующее - 1/2 от этой 1/2 или 1/4. Даже малая триада просит нас переместить эту вторую ноту на A # Bb, которая находится почти ровно на 3/16 (118,75% или 1,1875) от корня G.
Можно подумать, что было бы идеально создать шкалу, которая точно соответствует этим идеальным двоичным гармоникам. Было бы. Я пробовал это ... с 16 нотами ... по одной на каждую 1/16 шага. Звучало прекрасно. Гармоники были. Однако одна проблема ... каждый интервал был одинаковым, поэтому ... как указано выше, когда вы достигаете этой октавной частоты, которая в два раза больше корня, и начинаете другую октаву, вам нужно удваивать каждую последующую частоту ... и каждый интервал ... это означает, что есть заметный скачок между меньшими интервалами первой октавы и большими интервалами следующей. Урок ... что у вас вроде естьбыть логарифмическим по интервалу частот. Или, как в моей шкале «квазилогарифмическая», так что последний интервал одной октавы переходит к первому интервалу следующей октавы с небольшим «скачком» или без него.
Итак ... если эти двоичные дробные величины важны для гармонии, вопрос при оценке шкалы может быть сосредоточен вокруг того, какая логарифмическая шкала ближе всего подходит к важным двоичным отметкам гармоник. Моя «квазилогарифмическая» шкала «целое число / интервал целого числа» требует небольшого скачка, который нужно учитывать. Но в целом он достигает некоторых важных частот примерно с такой же точностью, как шкала 12TET. Мы оба примерно на одинаковую сумму от идеальной банкноты в 125%. 12TET очень близок к 150%, а мне немного не хватает. Но тогда ... Я намного ближе к отметке 175%, если кому-то это нужно! И мы оба почти точно достигли отметки 3/16.
Вот диаграмма, чтобы лучше понять, как ноты выглядят как 1/2, 1/4, 1/8 и 1/16 корня / октавы или двоичные!
Циркуляр сравнения гармоникЭта диаграмма показывает, как две логарифмические шкалы совпадают с не очень логарифмической схемой двоичных дробей.
На этой диаграмме мы видим, что шкала 12TET лучше справляется с достижением идеальных частот в начале (верхний левый квадрант). Но ... между моими нотами 3 и 7 у меня семь нот; по одному на каждую "идеальную" ноту, тогда как в 12TET их всего пять. Мои все немного далеки от идеала, но, по крайней мере, я следую идеалу с примечанием для каждого. Собственно с моей заметки 2.5 на 7.5 у меня по одному на каждую. Только в самом начале и в самом конце я не придерживаюсь идеала. Что не так важно, потому что эти ноты слишком близки к основной частоте, чтобы в любом случае добиться гармонии. Вам действительно нужно пройти эту точку на 3/16, прежде чем все начнет звучать близко к гармоническому. И выход за пределы этой отметки 175% / 3/4 также становится сомнительным. Итак, в целом моя шкала довольно точно соответствует бинарному гармоническому идеалу! Все идет нормально.
-----
C для аккордовНаблюдая за тем, как моя квазилогарифмическая шкала из 16 нот покрывает нелогарифмические 16 сегментов целого при делении на 1/2, 1/4, 1/8 1/16 лучше, чем традиционная 12-тональная система, я решил исследовать насколько близка эта гамма к созданию реальных трезвучий и аккордов. Это привело к еще одному интересному графику:
Таблица сравнения гармоникПоскольку моя шкала не совсем логарифмическая, но имеет этот крошечный скачок между октавами, процент увеличения от основного числа до гармонической ноты не всегда одинаков. Он может отличаться на другой процентный пункт или около того, в зависимости от того, пересекает ли триада этот октавный порог или нет. Строго логарифмическая прогрессия не будет иметь никакого «порога», который нужно пересечь, и процент увеличения будет одинаковым для любого корня. Но разброс моей шкалы минимален (или, судя по всему, на основании экспериментов со звуковыми файлами). Так что это в основном мои проценты увеличения по сравнению с процентом увеличения, необходимым для получения трезвучий и аккордов в системе 12TET.
Идея этой диаграммы состоит в том, что гармоники бинарны. Поэтому я разделил октаву на 16-е и рассчитал процент увеличения, необходимый для точного попадания каждой 16-й доли. Затем ... нанес на карту положение каждого типа аккорда, который я нашел, на большой таблице аккордов фортепиано. В таблице отображено 216 изображений аккордов (по 12 изображений для каждого из 18 типов аккордов). Но на самом деле картина одинакова для всех 12 нот. Этот образец можно увидеть по-разному. Я решил показать это как процент увеличения от основной ноты, чтобы увидеть, насколько близко этот процент приближается к предполагаемому идеалу двоичных приращений.
Как говорилось ранее, моя шкала немного дотягивает до критической отметки 1/2 или 150%. Но я думаю, что он все еще достаточно близок для работы (даже если он варьируется, чтобы быть немного дальше). И ... моя заметка 7.5 намного ближе к другой критической точке - отметке 3/4 или 175%. В общем, на этой диаграмме можно увидеть, что образцы аккордов группируются вокруг этих трех основных отметок: 1/4 или 125%, 1/2 или 150% и 3/4 или 175%. В этом есть смысл, если вы хотите сделать что-то гармоничное, вы комбинируете это с таким же рисунком ... только двойным, 1/2, 1/4 или 3/4. И если вы хотите сделать несколько интересных исключений, вы все равно не уходите слишком далеко от этих критических точек.
Итак, у меня есть двоичная шкала, потому что в ней 8 или 16 нот. И потому, что его основная структура использует двоичные приращения для определения этих 16 частот и интервалов. И потому, что в нем больше нот, соответствующих двоичной дробной структуре гармоник! Но ... как это звучит? Зайдите ЗДЕСЬ и поэкспериментируйте с некоторыми звуковыми файлами. Или сделайте инструмент, который может играть на этих нотах! А потом ... сделай мне одну !!
Двоичная шкала w GВот еще одна мандала, которая показывает, что эта новая двоичная шкала совмещена с частотами 12-тональной системы. К сожалению, это не совпадает с высшей точкой пентакля симметрии, существующей в 12-тональной системе. Эта мандала показывает ноты, расположенные на одинаковом расстоянии, и критические двоичные дробные точки гармонии логарифмически, а не наоборот (как показано на предыдущей диаграмме). Важно понимать, что середина круга - это не то же самое, что и середина частот. Используйте это, чтобы найти различные формы гармонии.
Все слова и изображения Copyright © 1980-2016, Гай Палм
Назад к деталям || Вернуться к книге | Вернуться к Таро | Главная | Карта сайта
Изучение Таро Использование Таро
Узоры Структура Резюме Философия заявка
Читать книгу! ...
Содержание удалено:
Купить книги
- Элементы ...
Времена года ...
Содержание удалено:
Купить книги
Ключевые модели ...
Ключевые диаграммы ...
Таблицы колод ...
Расположение палубы ...
Мандалы ...
Стихи ...
Искусство ...
Квинтаграммы ...
ХРАНИТЬ! МАГАЗИН! КУПИТЬ! ...
Содержание удалено:
Купить книги
Таро на костях ...
Мандала удачи ...
Мудры ...
Read more:
http://www.palmprints.com/guy/BookMusic ... z6imiqchwr
